Geogebra
Geogebra es un programa desarrollado para la enseñanza de la matemática escolar. Con Geogebra podremos enseñar de una manera sencilla y muy visible distintas nociones de geometría y álgebra, así como, facilitar el análisis.
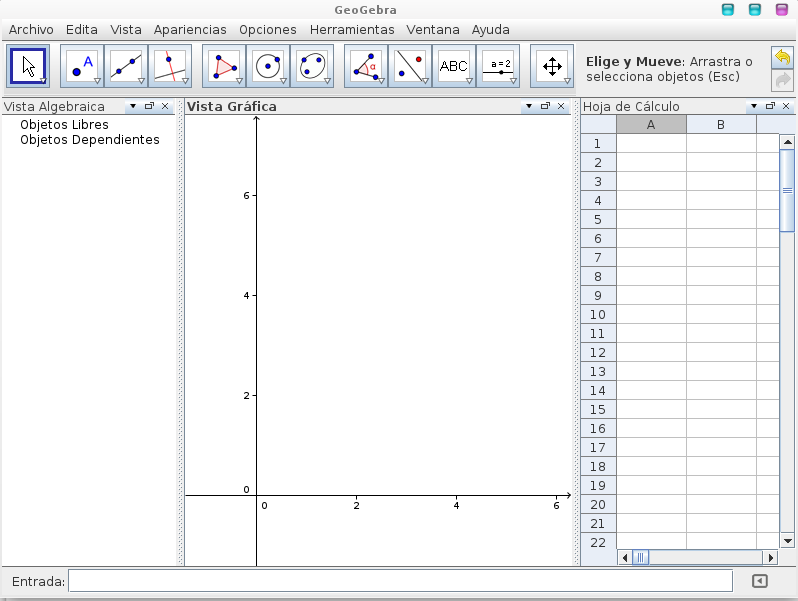
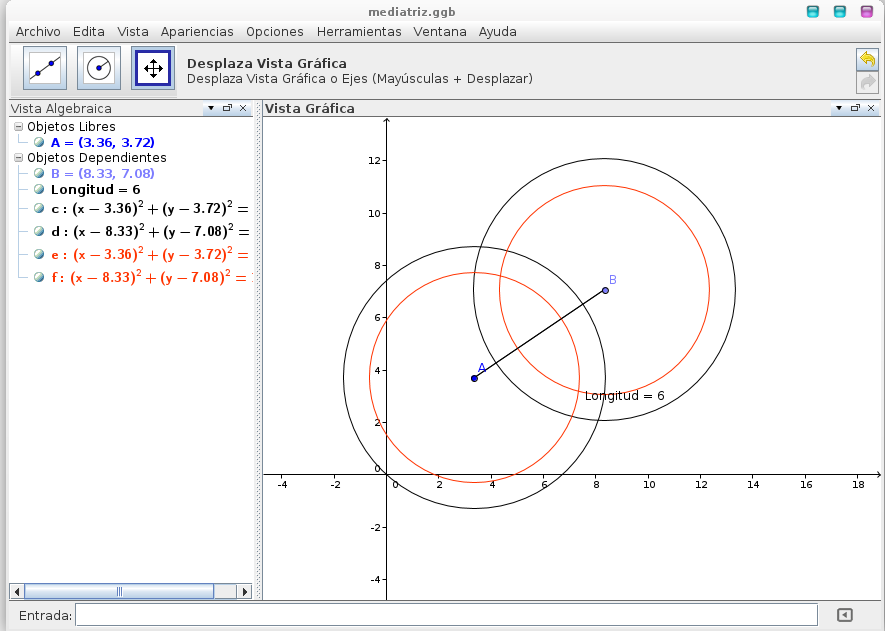
Como se observa en la imagen la interfaz es amigable.
En la parte superior tiene la barra de herramientas y la ayuda que indica qué es cada herramienta y como utilizarla.
A la izquierda se encuentra la vista algebraica todas las acciones ingresadas en cualquiera de los otros sectores aparecerán aquí, separadas para saber cuales son los objetos libres y cuales dependientes. Además, podremos hacer aparecer o desaparecer los objetos según nuestra conveniencia.
En el centro se encuentra la vista gráfica, donde una vez seleccionada la herramienta deseada aquí es donde se observan las figuras construidas. A la derecha se encuentra la hoja de calculo. Donde podremos realizar distintas operaciones y que aparezcan representados en la vista gráfica. En la parte inferior se encuentra la barra de entrada, aquí podemos realizar operaciones mediante comandos que aparecerán representadas tanto en la vista gráfica como en la algebráica.
Barra de herramientas
1) En el primer cuadro de herramientas se encuentran tres opciones. Elige y mueve te permite tomar un objeto libre de las construcciones realizadas y modificar la figura según se mueva ese punto, o bien, un objeto dependiente y moverlo dentro de la figura en la que se encuentra. Rota en torno a un punto, te permite luego de seleccionar un punto que hará de centro elegir otros puntos y que roten según el punto centro. Registro en una hoja de calculo, insertara en una hoja de calculo la ubicación del punto seleccionado
2) En el segundo cuadro de herramientas se encuentran las opciones de puntos tanto para realizar puntos libres como dentro de otras construcciones, además seleccionando dos elementos creara un punto en la intersección. En caso de ser necesario en este cuadro esta la opción de endosar o liberar un punto que este adherido en una figura.
3) La tercera caja tiene las herramientas para crear Rectas, semirrectas, segmentos y vectores. Los segmentos y vectores pueden calcularse según dos puntos o según su longitud.
4) En el cuarto cuadro se encuentran rectas particulares que se forman en base a otros objetos, como la bisectriz, la mediatriz, la paralela, la perpendicular, la tangente y la recta polar.
5) El quinto cuadro nos muestra las opciones para realizar distintos tipos de polígonos. Regulares, irregulares, rígidos (que no puedan modificar su forma luego) o vectoriales. Para realizarlos solamente es necesario elegir el tipo e ir creando los puntos hasta volver a marcar el punto de inicio. Para los polígonos regulares una vez seleccionada la herramienta se crean dos puntos luego se elige la cantidad de vértices que debe tener la figura deseada (contando los que forman los puntos realizados).
6) El sexto cuadro encontraremos las herramientas para el armado de circunferencias, con diferentes modos de armado, semicircunferencias, arcos de circunferencias y sectores circulares.
7) El séptimo cuadro finaliza con las secciones cónicas. En el mismo podremos realizar elipses, hipérbolas y parábolas.
8) El octavo cuadro nos brinda la posibilidad de crear ángulos mediante tres puntos, o bien, establecer el ángulo formado entre dos rectas, segmentos o vectores que ya estemos utilizando. Además encontraremos herramientas que nos proporcionaran datos útiles de nuestras construcciones para el análisis posterior.
9) En el noveno cuadro encontraremos herramientas para reflejar objetos en base a otros elementos.
10) El décimo cuadro encontraremos herramientas para agregar texto e imágenes a nuestro proyecto. Además tenemos herramientas para obtener información sobre relación entre dos objetos, calculo de probabilidades e inspección de función.
11) En este cuadro se encuentran mas herramientas que nos brindan información y herramientas para realizar acciones dinámicas.
12) El ultimo cuadro nos ofrece herramientas para poder visualizar de mejor manera las construcciones realizadas.
Barra de Entrada
En la barra de entrada podemos ingresar distintos comandos. Con la ayuda de estos se pueden crear nuevos objetos o modificar los existentes, que serán observados en la vista gráfica.
Ejemplos Para crear un punto “A” en la ubicación (4,3) solo necesitamos ingresarlo en la Barra de entrada de la siguiente manera
(Recordar que los punto en el Geogebra se representan con letras mayúsculas)
Para realizar una recta:
De esta manera, Geogebra le generara el nombre a la recta.
Si se desea se le puede asignar un nombre manualmente agregando antes el nombre seguido de “:”. Por ejemplo:
De esta manera le asignamos el nombre recta3 a la recta anterior.
Se pueden ingresar funciones por ejemplo:
Con el comando segmento se pueden crear segmentos, por ejemplo, si quiero crear un segmento entre un punto A y un punto B lo haría de la siguiente manera.
Al ingresar los segmentos el mismo programa nos facilitara la resolución de los mismo, ofreciéndonos las opciones que podemos tener en cada caso.
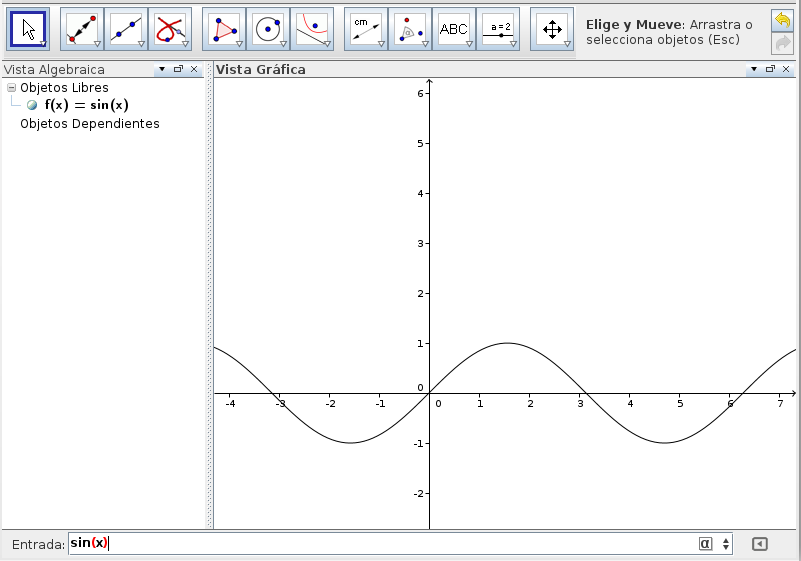
Mediante la barra de entrada podemos formar distintos objetos que serian mas complicados realizarlos de forma manual. Por ejemplo el seno(x)
El Geogebra cuenta con mas de mil comandos para realizar todo tipo de construcciones algebraicas. El siguiente link muestra todas las variables con las que trabaja el programa.
https://wiki.geogebra.org/es/Comandos
Estudio de mediatriz
Mostraremos la mediatriz de un segmento de 6 cm realizando circunferencias de mismo radio en sus extremos.
Primero realizaremos el proyecto en el cual los alumnos luego podrán hacer distintos ejercicios. Para ello.
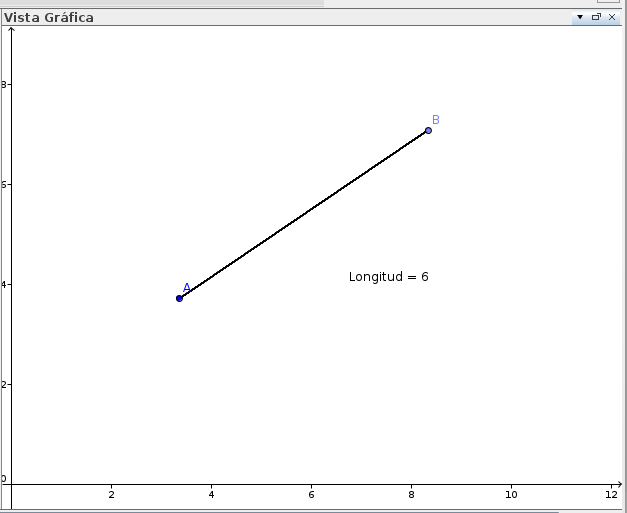
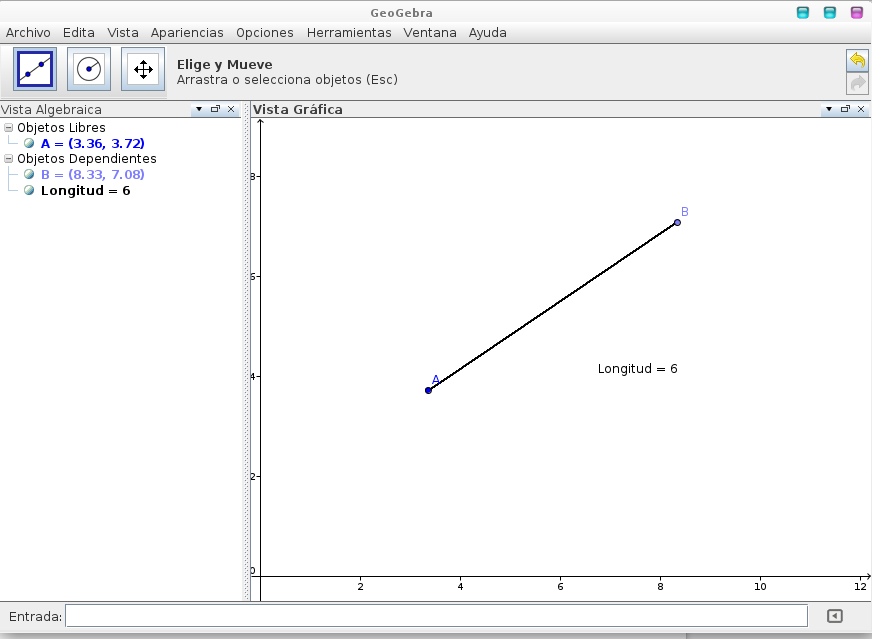
Creamos un punto A en la vista gráfica con la herramienta nuevo punto. Ubicada en el segundo cuadro. Con la herramienta Segmento dado punto extremo y longitud que se encuentra en el tercer cuadro. Seleccionamos el punto A y definimos la longitud de seis cm. Se creara el segmento AB. Con la herramienta elige y mueve podemos mover el punto B hacia arriba o abajo sin modificar la longitud del segmento. Con la herramienta distancia o longitud que se encuentra en el octavo casillero de herramientas podremos agregar un rotulo que diga la longitud del segmento.
En este momento tenemos la siguiente construcción
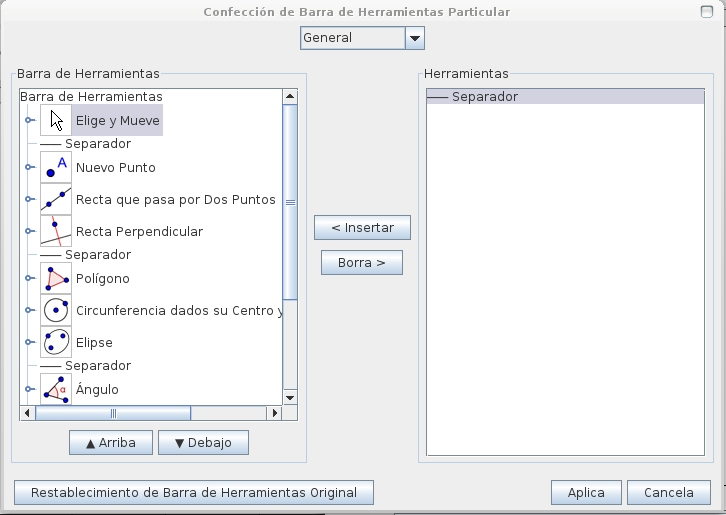
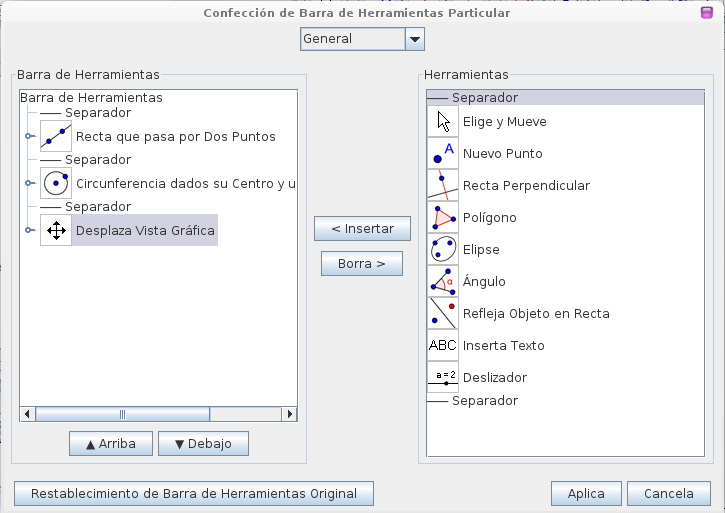
Ahora guardaremos el proyecto para que luego los alumnos puedan realizar ellos mismos los ejercicios. Antes de esto podemos dejar únicamente las herramientas que serán útiles para este trabajo, para ello vamos a la solapa herramientas ubicada en la parte superior del Geogebra y seleccionamos la opción confección de barra de herramienta particular. Se abrirá el siguiente recuadro.
Aquí borramos todas las herramientas salvo, Recta que pasa por Dos puntos, Circunferencia dado su centro y uno de sus puntos y Desplaza vista gráfica.
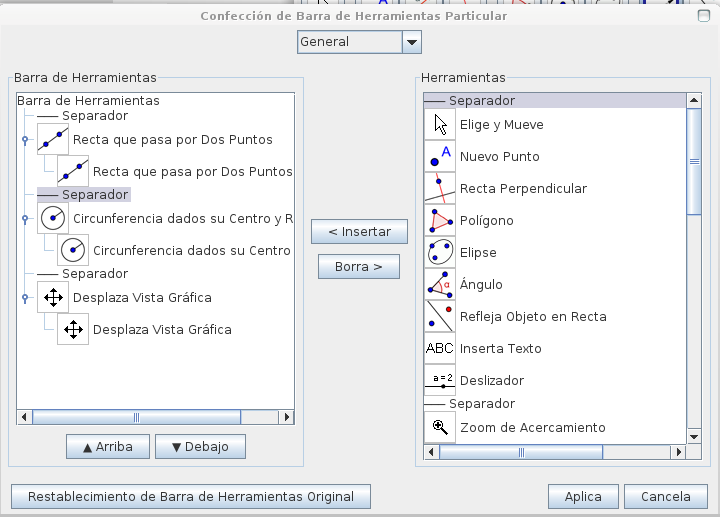
Luego, tocamos los pequeños círculos al lado de cada herramienta y se abrirán otras opciones. De las herramientas de Rectas borramos todas las opciones salvo la que se llama Recta que pasa por dos puntos. De las herramientas de Circunferencia dejamos solamente Circunferencia dado su centro y radio. De las herramientas de desplazamiento dejamos únicamente Desplaza vista Gráfica.
cerramos la ventana de Confección de Barra de Herramientas Particular.
Actualmente nuestro Geogebra se vera de esta manera:
Ahora si, lo podemos guardar yendo a la solapa Archivo y luego a guardar. Podemos elegir el nombre del archivo que queramos. Al abrir el archivo solamente se verán las herramientas elegidas anteriormente para que le resulte mas fácil al estudiante encontrarlas.
Le pasamos un archivo que puede realizarse confeccionado el archivo se les puede dar el siguiente ejercicio a los alumnos para descubran ellos solos la forma de calcular la mediatriz y el punto medio de un segmento.
Dado un segmento AB de 6 cm de longitud.
A) Marcar todos los puntos que estén a 5 cm de A.
Marcar todos los puntos que estén a 5 cm de B. ¿Existen puntos que estén a 5 cm de A y a su vez, a 4 cm de B? ¿Cuantos son?
B) Realizar lo mismo realizado en el punto A) pero con los puntos que se encuentren a 4 cm de A y de B
¿Existen puntos que estén a 4 cm de A y a su vez, a 5 cm de B? ¿Cuantos son?
C) ¿Se puede realizar una recta que pase por puntos que estén simultáneamente a 5 cm de A y de B y por los puntos que estén simultáneamente a 4 cm de A y de B? ¿En que punto se cruza con el segmento AB?
D) Marcar todos los puntos que estén a 3 cm de A
Marcar todos los puntos que estén a 3 cm de A
¿En que punto se tocan las circunferencias? ¿Porque?
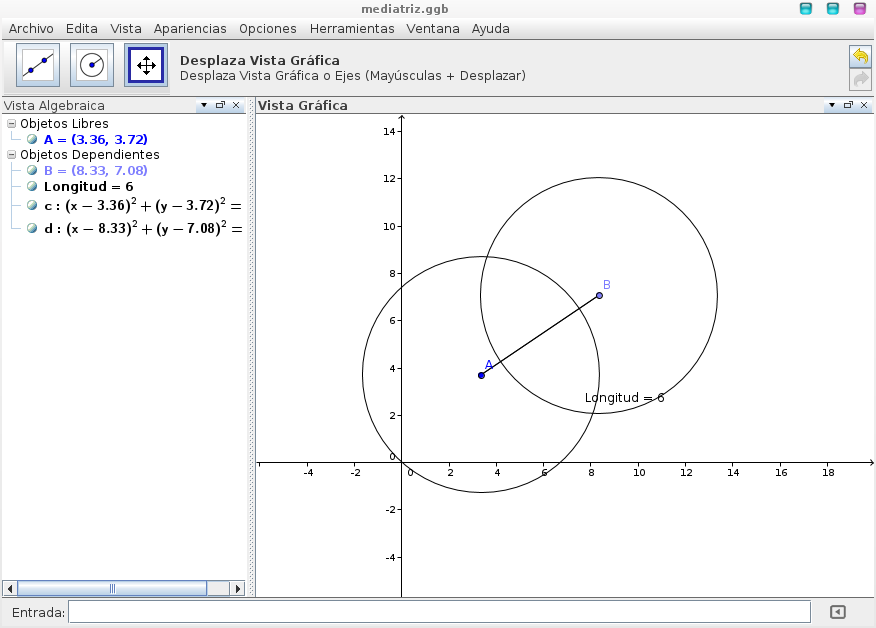
Para realizar este ejercicio los alumnos deben . Abrir el archivo realizado con anterioridad. Seleccionar la herramienta Circunferencia dados su centro y radio, con ella tocar el punto A y darle un valor igual a 5 cuando el programa pregunte la medida del radio. Realizar lo mismo con el punto B.
Luego de responder que tienen dos puntos en común. Se realizara lo mismo que al principio pero con el radio igual a 4.
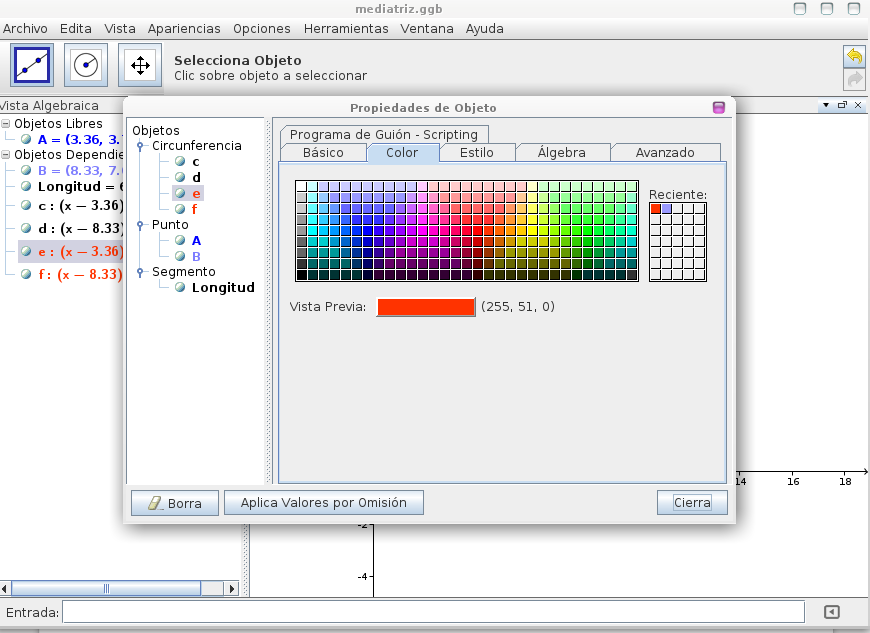
Se les puede decir que modifiquen el color de las circunferencias interiores para que sea mas fácil visualizar cual es cual. Para ello colocamos el cursor sobre una de las circunferencia y apretamos el botón derecho del mousse y seleccionamos la opción propiedades del objeto. Allí vamos a la solapa color y seleccionamos el color que deseamos. Hacemos lo mismo con la otra circunferencia de igual radio y al seleccionar color en el cuadro de reciente nos aparecerá el color que utilizamos en la primera.
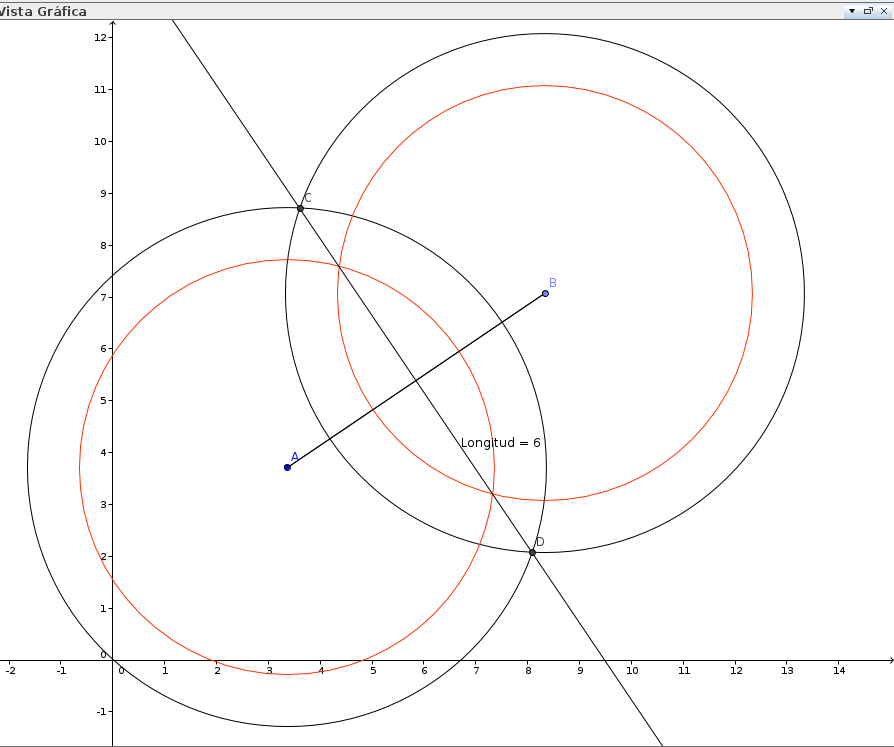
Una vez que se construyeron las cuatro circunferencias se debe realizar la recta solicitada en el punto C). Para ello seleccionamos la herramienta Recta que pasa por dos puntos y apretamos en la intersecciones de las circunferencias de 5 cm.
Los alumnos podrán sacar sus propias conclusiones de por que la recta se cruza por los cuatro puntos donde se cruzan las circunferencias y cual es el punto donde cruza al segmento.
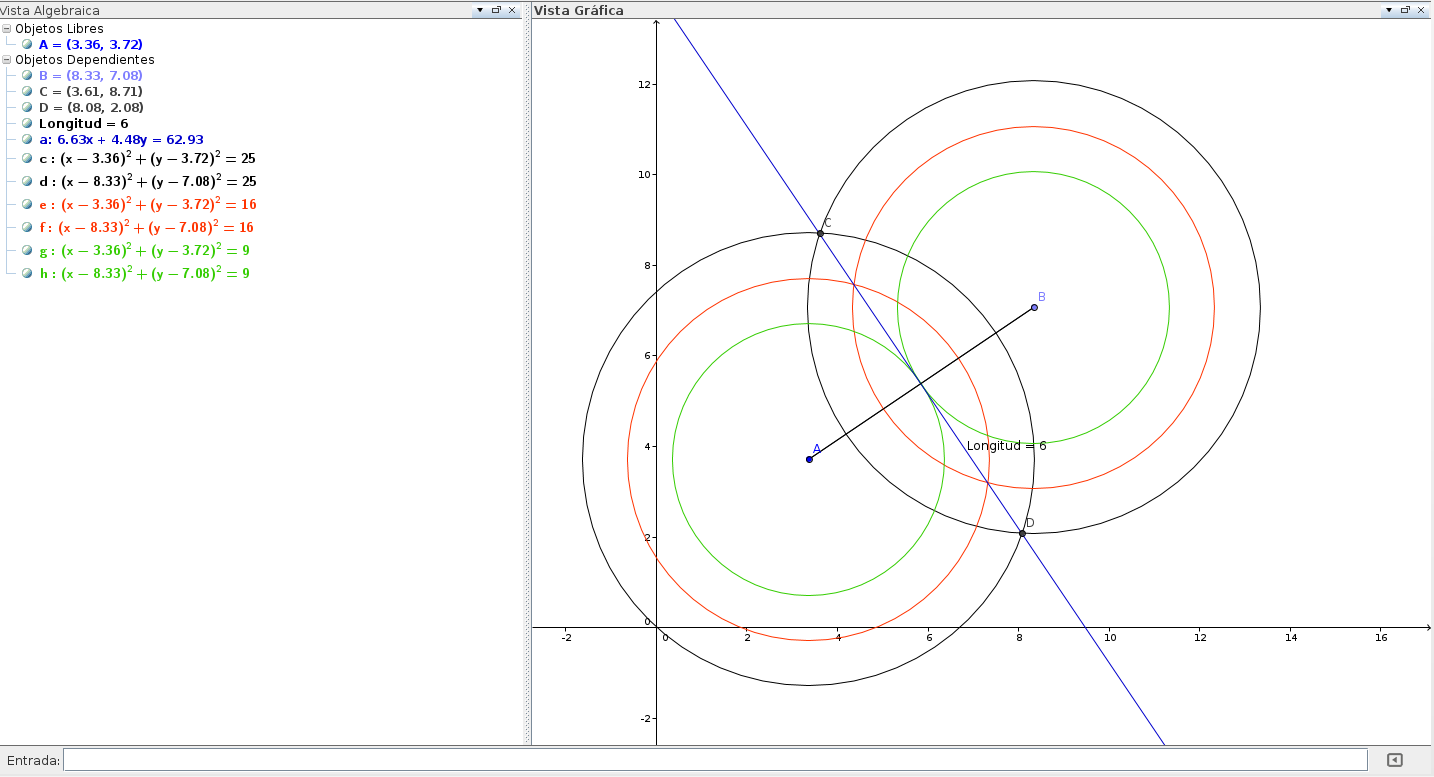
Finalmente para dejar en claro que cruza el punto medio del segmento y que la recta es la mediatriz se realiza el punto D) realizando las circunferencias solicitadas.
Podemos modificar los colores de las construcciones para una mejor visualización.
Suma de los ángulos internos del triangulo
En esta propuesta los alumnos podrán observar que la suma de los ángulos internos de todo triangulo suman 180°.
Primero, realizamos el proyecto para que luego los alumnos puedan trabajar en él.
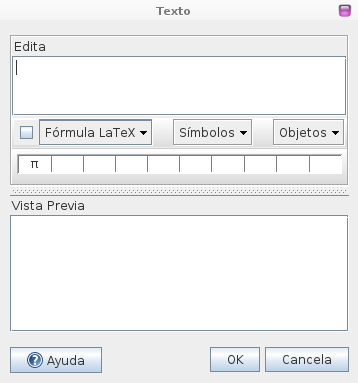
Creamos un triangulo cualquiera con la herramienta polígono que se encuentra en el quinto cuadro de herramientas. Con la herramienta ángulo que se encuentra en la octava caja de herramientas, mostraremos los ángulos internos del triangulo. Para ello, elegiremos la herramienta y presionaremos el botón izquierdo del mousse dentro del polígono. Ahora seleccionamos la herramienta Inserta texto y presionamos el botón izquierdo del mousse en algún lugar de la vista gráfica lejos del triangulo. Nos aparecerá el siguiente cuadro.
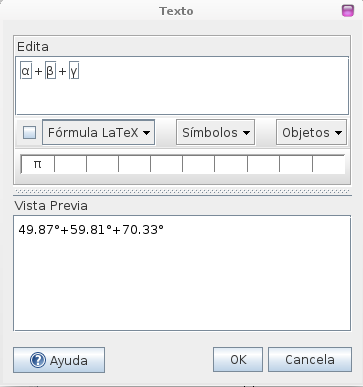
Aquí tocamos el botón izquierdo del mousse sobre uno de los ángulos internos del triangulo, para seleccionarlo luego presionamos la tecla + del teclado, después seleccionamos otro de los ángulos de la misma manera que el primero y luego nuevamente +, finalmente seleccionamos el ultimo ángulo interno que nos falta del triangulo y tocamos el botón OK.
El cuadro de texto nos quedara de la siguiente manera.
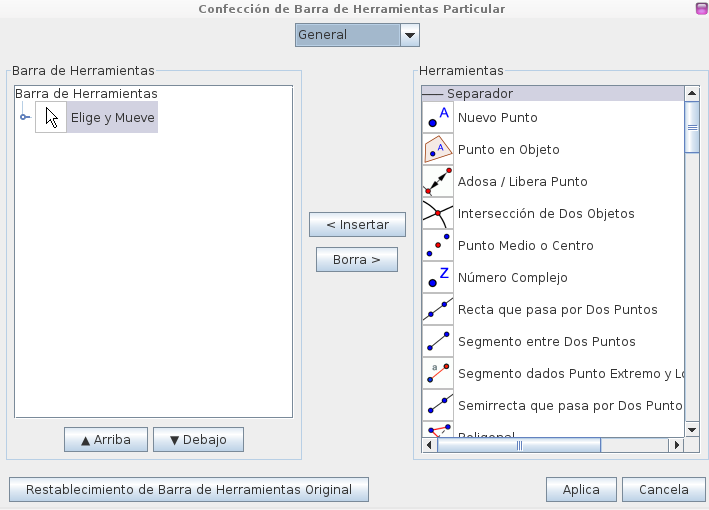
Antes de guardarlo eliminaremos todas las herramientas que no se utilizaran en la muestra que realizara el alumno. Para ello vamos a la solapa herramientas ubicada en la parte superior del Geogebra y seleccionamos la opción confección de barra de herramienta particular. Se abrirá el siguiente recuadro.
Aquí borramos las todas las herramientas salvo, Elige y mueve.
Luego, tocamos el pequeño círculo al lado de la herramienta y se abrirán otras opciones, borramos todas las opciones menos la que dice Elige y mueve.
Presionamos Aplica y después cerramos el cuadro.
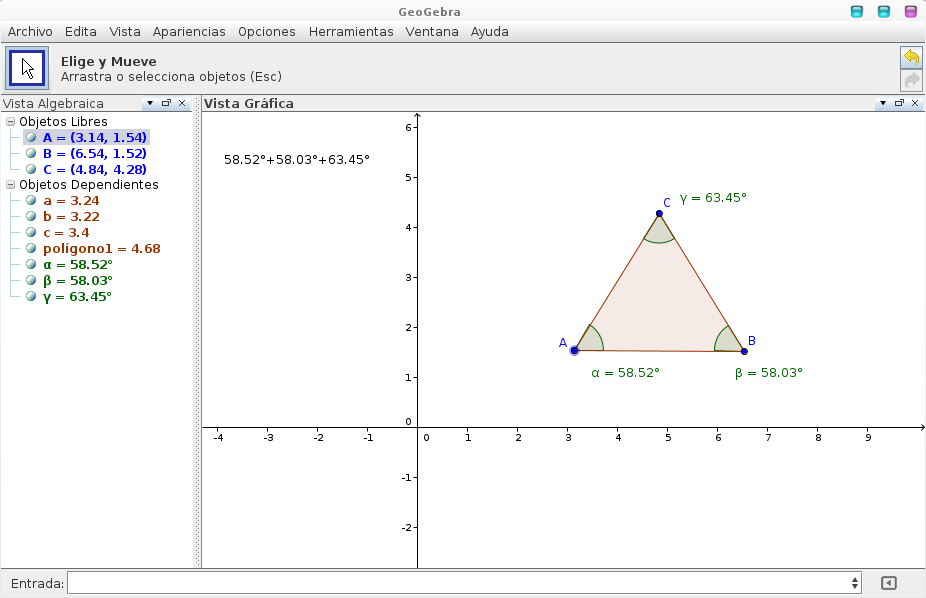
El proyecto listo para guardar, deberá verse similar a la siguiente imagen:
Ahora lo guardamos dirigiéndonos a Archivo, presionando guardar y asignándole el nombre deseado.
Un ejercicio que se puede proponer a los alumnos con este archivo es que muevan los vértices del triangulo con la herramienta Elige y mueve y que sumen los valores de los ángulos internos que se forman. Luego, que repitan la acción cuantas veces deseen. De esta manera notaran que no importa donde ubiquen los puntos los ángulos internos sumaran siempre 180°.
En la página de [de Innovación] se encuentran muchas más propuestas para trabajar con Geogebra.